LIMITES
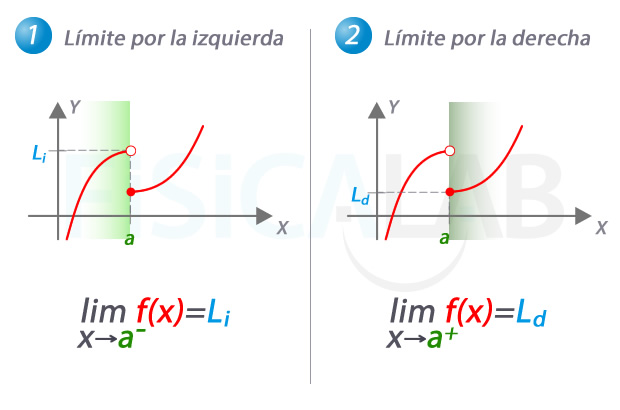
Una definición informal del límite matemático indica que el límite de una función f(x) es T cuando x tiende a s, siempre que se puede hallar para cada ocasión un x cerca de s de manera tal que el valor de f(x)sea tan cercano a T como se pretenda.

FUENTE: https://definicion.de/limites-matematicos/

                                                   https://miprofe.com/limites-introduccion/

PROBLEMA 1 

https://drive.google.com/file/d/1BvoU3qm0Aq7Jso9JO0tNdSaCYaQQU7R8/view?usp=sharing

PROBLEMA 2

https://drive.google.com/file/d/1-BjlfTdS5ZdSFoRUGtEcHyrnw0qftcWY/view?usp=sharing

EJERCICIO 1 

https://drive.google.com/file/d/1s0SbiNMOpygqYsE5yd4YFoZqOT6SU2y4/view?usp=sharing 

LIMITES LATERALES

Para que exista el límite de una función, deben existir los límites laterales y coincidir.

El significado de los signos en la notación para límites laterales se interpreta de la siguiente manera

• x ® a^- significa que x tiende a a tomando valores menores que a, es decir valores que se encuentran a su izquierda.
• x ® a⁺ significa que x tiende a a tomando valores mayores que a, es decir valores que se encuentran a su derecha. 

FUENTE: https://www.fca.unl.edu.ar/Limite/2.2%20L%EDmiteslaterales.htm

https://www.fisicalab.com/apartado/limites-laterales#contenidos



         PROBLEMA 1

     https://drive.google.com/file/d/1UjWBsLDMK7Vu3U9rtnLlDEO10HCKzlfh/view?usp=sharing

EJERCICIO 1

https://drive.google.com/file/d/1uBS3FJZOAAkQ701Pa8I5PDDvny6Gi_T_/view?usp=sharing

PROBLEMA 2
https://drive.google.com/file/d/19A4q0Axqha_CoJKAwofjwiUXkqUt33g7/view?usp=sharing

En esta oportunidad presentamos el tema Composición de Funciones, que son aquellas formadas por la composición o aplicación sucesiva de otras dos funciones.
De esta manera, se aplica sobre el argumento la función más próxima al mismo, y al resultado del cálculo obtenido se le aplica finalmente la función restante.
Los autores del presente blog son:

- NÚÑEZ UGAZ SHANIA
- CEDEÑO RAVINES BRYAN
- VARGAS PANDURO GREGORI
- TORRES VENTURA SHIRLEY

OBJETIVOS DEL TEMA 

*Pretendemos que a base de los ejercicios tengamos los conocimientos básicos sobre la composición de funciones y poder lograr su interpretación. 

*En un futuro nos ayudará  a reconocer situaciones cotidianas que requieran operaciones elementales.

OBJETIVOS DEL BLOG 

* El objetivo  del blog es lograr que las personas cambien su manera de pensar de que no solo se puede aprender de una sola manera, ya que ahora con  toda la tecnología que contamos podemos adquirir nuevos conocimientos a través de un blog. 

*A través del blog queremos compartir conocimiento e intercambiar información. 

 

EJERCICIOS SOBRE COMPOSICIÓN  DE FUNCIONES:

Ejercicio 1: 

Encuentre la función compuesta de f(g(x)) , donde f(u)=u²+3u+1 y g(x)=x+1 

Solución: 

Reemplace u por x+1 en la formula de f(u) para obtener 

f(g(x))= (x+1)² + 3(x+1) + 1

           = (x²+2x+1) + (3x+3) + 1

           = x² + 5x + 5

FUENTE: MATEMÁTICAS APLICADAS A LA ADMINISTRACIÓN Y LOS NEGOCIOS (510-HOFF2014) 

Ejercicio 2:

Dada g(x) = 3x²- 2x + 5, evalúe a) g(1 + h) ; b) g(1) + g(h) ; c) [g(x + h) - g(x)] /h.

Solución: Tenemos 

g(x) = 3x²- 2x + 5 

a) Con el propósito de evaluar g(1+h), debemos sustituir x en la ecuación (2) por 1 + h. 

g(1 + h) = 3(1 + h)² – 2(1 + h) + 5

             = 3(1 + 2h + h²) - 2 - 2h + 5

             = 3h² + 4h + 6

b) Reemplazando x por1 y h. respectivamente, enla ecuación(2) obtenemos 

g(1) = 3(1²) – 2(1) + 5 = 3 – 2 + 5 = 6

y así mismo

g(h) = 3h² – 2h + 5

Por tanto, 

g(1) + g(h) = 6 + 3h² – 2h + 5 = 3h² – 2h + 11 

c) Reemplazando el argumento x en la ecuación (2) or x + h,  tenemos las siguientes igualdades: 

g(x + h) = 3(x + h)² – 2(x + h) + 5

                = 3(x² + 2xh + h²) – 2x – 2h + 5

                = 2x² + 2x - 5 + h(3h + 6x – 2)

En consecuencia, 

1/h [g(x + h) – g(x)]

                = 1/h [3x² – 2x + 5 + h(3h + 6x – 2) – (3x² – 2x + 5]

                = 3 + 6x - 2

BIBLIOGRAFÍA: MATEMÁTICAS APLICADAS A LA ADMINISTRACIÓN Y A LA ECONOMÍA (510-ARYA/A2009) 

Ejercicio 3: 

Evalúe F(0), F(1) Y F(4) para la función F definida por

Solución  Primero reemplace x por 0:

 

Después reemplace x por 1:

Por último, reemplace x por 4:

                     

No definido

F(4) no existe; en otras palabras, 4 no está en el dominio de F

FUENTE: MATEMÁTICAS APLICADAS A LA ADMINISTRACIÓN Y A LA ECONOMÍA (510-ARYA/A2009)

       

¿QUÉ ES UNA COMPOSICIÓN DE FUNCIONES? 

La composición de funciones es la imagen resultado de la aplicación sucesiva de dos o más funciones sobre un mismo elemento x. Siendo f y g dos funciones, se define la composición de dos funciones (denotada por g o f) como: 

La composición de funciones se realiza aplicando dichas funciones en orden de derecha a izquierda, de manera que en (g o f)(x) primero actúa la función f y luego la g sobre f(x).

https://www.universoformulas.com/matematicas/analisis/composicion-funciones/

VIDEO N°1

https://drive.google.com/file/d/1PneMdlIrN7wHREuvqZA8IM7Ur62JrvSs/view?usp=sharing

VIDEO N°2 

https://drive.google.com/file/d/1Aud9H8T3ub125Cup_GCv-6iurElF6iZb/view?usp=sharing